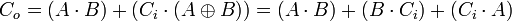Wanda asri putra

Minggu, 04 Juli 2010

REGISTER BUFFER TERKENDALI

Register Buffer Terkendali adalah register buffer yang ditambah dengan beberapa gerbang logika dasar AND, OR, dan NOT. Gambar rangkaian menunjukkan sebuah Register buffer terkendali dengan CLR aktif tinggi. Apabila CLR = 1, maka akan terjadi reset pada flip-flop dan data yang tersimpan (Q) menjadi 0000. dan ketika CLR = 0, register siap beroperasi kembali.
Sinyal kendali LOAD adalah input kendali yang menentukan operasi rangkaian.Ketika LOAD = 0, semua input data tidak diizinkan masuk, artinya flip-flop mengisolasi input data atau menahan semua data yang ada di dalamnya. Dengan kata lain, register tidak berubah selama LOAD = 0. Ketika LOAD = 1, semua input data akan diterima oleh register. Ketika LOAD kembali = 0, maka input data yang diterima register tadi akan tersimpan dengan aman tanpa gangguan perubahan input.

II. REGISTER GESER TERKENDALI
Sebuah register geser terkendali (controlled shift register) mempunyai masukan-masukan kendali yang mengatur operasi rangkaian pada pulsa pendetak yang berikutnya. Jika SHL rendah maka sinyal SHL tinggi. Keadaan ini membuat setiap keluaran flip-flop masuk kembali ke masukan datanya. Karena itu data tetap tersimpan pada setiap flip-flop pada waktu pulsa-pulsa detak tiba.
Jika SHL tinggi, Din akan masuk ke dalam flip-flop paling kanan, Q0 masuk ke dalam flip-flop kedua, Q1 masuk ke dalam flip-flop ketiga, dst. Dengan demikian rangkaian bertindak sebagai register geser kiri.

Senin, 21 Juni 2010

tugas 7

RANGKAIAN UP/DOWN COUNTER

Rangkaian Up/Down Counter merupakan gabungan dari Up Counter dan Down Counter. Rangkaian ini dapat menghitung bergantian antara Up dan Down karena adanya input eksternal sebagai control yang menentukan saat menghitung Up atau Down. Pada gambar 4.4 ditunjukkan rangkaian Up/Down Counter Sinkron 3 bit. Jika input CNTRL bernilai ‘1’ maka Counter akan menghitung naik (UP), sedangkan jika input CNTRL bernilai ‘0’, Counter akan menghitung turun (DOWN).

Minggu, 06 Juni 2010

tuga 6

Penjumlah dan Pengurang Komplemen 2

Rangkaian logika yang dapat berfungsi untuk menjumlahkan atau mengurangkan dua
bilangan biner
Jika SUB = 1 maka FA akan menghasilkan S = A + B + 1 = A + B’
B’ merpresentasikan bilangan negatif, sehingga S = A – B.

Minggu, 02 Mei 2010

tugas 5

Penjumlah atau Adder adalah komponen elektronika digital yang dipakai untuk menjumlahkan dua buah angka dalam sistem bilangan biner. Dalam komputer dan mikroprosesor, Adder biasanya berada di bagian ALU (Arithmetic Logic Unit). Sistem bilangan yang dipakai dalam proses penjumlahan, selain bilangan biner, juga 2's complement untuk bilangan negatif, bilangan BCD (binary-coded decimal), dan excess-3. Jika sistem bilangan yang dipakai adalah 2's complement, maka proses operasi penjumlahan dan operasi pengurangan akan sangat mudah dilakukan.

Diagram sirkuit Half-Adder

Pembicaraan mengenai Adder biasanya dimulai dari Half-Adder, kemudian Full-Adder, dan yang ketiga adalah Ripple-Carry-Adder. Pada Half-Adder, berdasarkan dua input A dan B, maka output Sum, S dari Adder ini akan dihitung berdasarkan operasi XOR dari A dan B. Selain output S, ada satu output yang lain yang dikenal sebagai C atau Carry, dan C ini dihitung berdasarkan operasi AND dari A dan B. Pada prinsipnya output S menyatakan penjumlahan bilangan pada input A dan B, sedangkan output C menyatakan MSB (most significant bit atau carry bit) dari hasil jumlah itu.

$S = (A \oplus B)$

$C = (A \cdot B)$

Tabel logika/kebenaran dari Half-Adder akan mengikuti seperti berikut:

Input		Output
A	B	C	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Diagram blok Full-Adder

Rangkaian Full-Adder, pada prinsipnya bekerja seperti Half-Adder, tetapi mampu menampung bilangan Carry dari hasil penjumlahan sebelumnya. Jadi jumlah inputnya ada 3: A, B dan Ci, sementara bagian output ada 2: S dan Co. Ci ini dipakai untuk menampung bit Carry dari penjumlahan sebelumnya.

$S = (A \oplus B) \oplus C_i$

$C_o = (A \cdot B) + (C_i \cdot (A \oplus B)) = (A \cdot B) + (B \cdot C_i) + (C_i \cdot A)$

Diagram sirkuit Full-Adder

Input			Output
$A$	$B$	$C i$	$C o$	$S$
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Rangkaian dari n buah Full-Adder bisa dipakai untuk menjumlahkan n bit bilangan biner. Maka dalam hal ini, kita akan memperoleh rangkaian yang disebut Ripple-Carry-Adder.

Minggu, 18 April 2010

tugas 4 ( hukum aljabar)

Soal :

1. Give the relationship that represents the dual of the Boolean property A + 1 = 1?
(Note: * = AND, + = OR and ' = NOT)

1. A * 1 = 1

2. A * 0 = 0 (Jawabanya)

3. A + 0 = 0

4. A * A = A

5. A * 1 = 1

2. Give the best definition of a literal?

1. A Boolean variable

2. The complement of a Boolean variable (Jawabannya)

3. 1 or 2

4. A Boolean variable interpreted literally

5. The actual understanding of a Boolean variable

3. Simplify the Boolean expression (A+B+C)(D+E)' + (A+B+C)(D+E) and choose the best answer.

1. A + B + C (Jawabannya)

2. D + E

3. A’B’C’

4. D’E’

5. None of the above

4.Which of the following relationships represents the dual of the Boolean property x + x'y = x + y?

1. x’(x+y’) = x’y’ (Jawabannya)

2 x(x’y) = xy

3. x*x’ + y = xy

4. x’(xy’) = x’y’

5. x(x’ + y) = xy

5.Given the function F(X,Y,Z) = XZ + Z(X'+ XY), the equivalent most simplified Boolean representation for F is:

1. Z + YZ

2. Z + XYZ (Jawabannya)

3. XZ

4. X + YZ

5. None of the above

6. Which of the following Boolean functions is algebraically complete?

1. F = xy (Jawabannya)

2. F = x + y

3. F = x’

4. F = xy +yz

5. F = x + y’

7. Simplification of the Boolean expression (A + B)'(C + D + E)' + (A + B)' yields which of the following results?

1. A + B

2. A’B’ (Jawabannya)

3. C + D + E

4. C’D’E’

5. A’B’C’D’E’

8. Given that F = A'B'+ C'+ D'+ E', which of the following represent the only correct expression for F'?

1. F’= A+B+C+D+E

2. F’= ABCDE

3. F’= AB(C+D+E)

4. F’= AB+C’+D’+E’

5. F’= (A+B)CDE (Jawabannya)

9. An equivalent representation for the Boolean expression A' + 1 is

1. A

2. A’

3. 1 (Jawabannya)

4. 0

10. Simplification of the Boolean expression AB + ABC + ABCD + ABCDE + ABCDEF yields which of the following results?

1. ABCDEF

2.AB (Jawabannya)

3.AB +CD +EF

4. A+B+C+D+E+F

5.A+B(C+D(E+F))

Hukum Aljabar Boolean

1. HUKUM KOMUTATIF

a. A + B = B + A

A + B

B + A

b. A . B = B . A

A . B

B . A

2. HUKUM ASOSIATIF

a. (A + B) + C = A +(B + C)

A + B

B + C

(A + B) + C

A + (B + C)

b. (A . B) . C = A . (B . C)

A . B

B . C

(A . B) . C

A . (B . C)

3. HUKUM DISTRIBUTIF

a. A . (B + C) = A . B + A . C

B + C

A . B

A . C

A.(B+C)

A.B + A.C

b. A + (B . C) = (A + B)(A + C)

B . C

A + B

A + C

A+(B.C)

(A+B)(A+C)

4. HUKUM IDENTITY

a. A + A = A

A + A

b. A . A = A

A . A

5. a. A . B + A . B’ = A

B’

A . B

A . B’

A.B + A.B’

b.(A +B)(A + B’) = A

B’

A + B

A + B’

(A+B)(A+B’)

6. HUKUM REDUDANSI

a. A + A . B = A

A . B

A + A .B

b. A (A + B) = A

A + B

A (A+B)

7. a. 0 + A = A

0 + A

b.0 .A = 0

0 . A

8. a. 1 + A = 1

1 + A

b. 1 . A = A

1 . A

9. a. A’ + A =1

A’

A’ + A

b.A’ .A =0

A’

A’ . A

10. a. A + A’ . B = A + B

A’

A’ . B

A + A’.B

A + B

b.A(A’ +B) = A . B

A’

A’ + B

A (A’+B)

A . B

11. THEOREMA DE MORGAN

a. (A + B)’ =A’ . B’

A’

B’

A + B

(A +B)’

A’ . B’

b. (A .B)’ = A’ + B’

A’

B’

A . B

(A .B)’

A’ + B’